In diesem Blog war ja schon mehrfach die Rede von den Unterschieden zwischen algorithmischem Vorgehen und menschlichem Denken. Insbesondere wird dem menschlichen Denken von mancher Seite vorgeworfen, nicht besonders logisch zu sein, und clever gemachte Experimente zeigen, dass wir uns regelmäßig „in die Denkfalle locken“ lassen. Andererseits gibt es Wissenschaftler wie Gerd Gigerenzer, die die menschliche Intuition vehement verteidigen gegen solche Angriffe verteidigen.
In diesem Zusammenhang bin ich kürzlich auf das Buch „What makes us smart“ des Harvard-Psychologen Samuel Gershman gestoßen, das in der Diskussion einen ganz anderen Ton anschlägt. Es stellt nämlich die These auf, dass das menschliche Denken sogar ausgesprochen rational ist, wenn man sich erst einmal bemüht, all die Faktoren zu berücksichtigen, die wir in unsere Entscheidungen mit einbeziehen, oft ohne es überhaupt zu bemerken. Er verwendet dabei die Argumentation des Bayesianismus, der das Verhalten des Gehirns mit (subjektiven) Wahrscheinlichkeitsannahmen zu erklären versucht und der in der Kognitionswissenschaft in letzter Zeit große Bedeutung gewonnen hat. Leider ist das Buch von Gershman alles andere als leicht zu lesen, weil er seine Ideen für den Quereinsteiger zu wenig ausführt, aber es ist prall gefüllt mit interessanten Denkanstößen, die er aus verschiedensten Disziplinen der Kognitionslehre zusammengesucht hat.

Im Folgenden möchte ich einmal ein Beispiel für diese Denkweise heraussuchen, die unmittelbar einleuchtet und aufzeigt, warum auch vollkommen rationale Entscheider zu Fehlentscheidungen kommen können.
Eine einfache Informationskaskade
Betrachten wir einmal ein etwas formalisiertes Beispiel. Es gibt zwei Urnen A und B, die mit roten und blauen Kugeln gefüllt sind. Urne A enthält zwei rote und eine blaue Kugel, Urne B enthält eine rote und zwei blaue Kugeln:
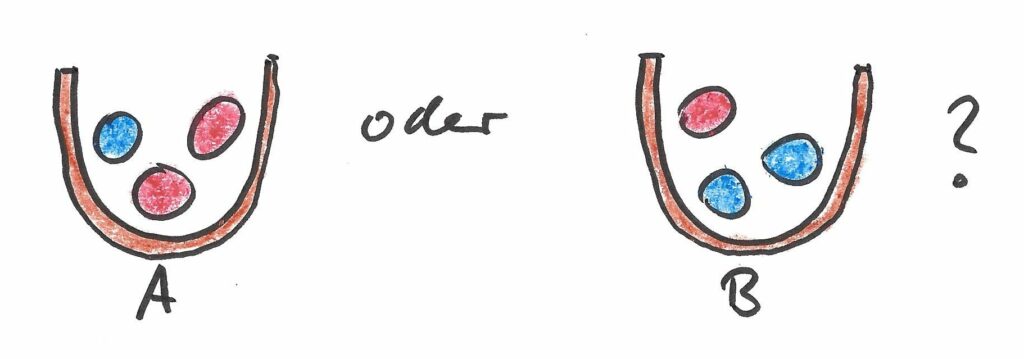
Nun stehen einige Entscheider vor der Frage, ob eine Urne, deren Inhalt sie nicht sehen können, vom Typ A oder vom Typ B ist. Dazu dürfen Sie jeweils eine Kugel (verdeckt für die anderen) ziehen, dann müssen sie einen Tipp abgeben, um welchen Urnentyp es sich handelt. Die Kugel wird dann wieder in die Urne zurückgelegt, und es kommt der nächste Entscheider an die Reihe. Dieser hat nun aber den Vorteil, dass er das Urteil seiner Vorgänger kennt.
Nehmen wir einmal an, dass es sich in Wahrheit um eine Urne vom Typ A handelt, dass aber der erste Entscheider eine blaue Kugel gezogen hat. Als rationaler Entscheider wird er als Ergebnis „Typ B“ verkünden (was falsch ist, aber das kann er ja mit seinem Informationsstand nicht wissen). Nehmen wir nun weiterhin an, dass auch der zweite Entscheider eine blaue Kugel zieht. Aus seinem Ergebnis und der Aussage des ersten Entscheiders folgert er natürlich ebenfalls (fälschlicherweise), dass es sich um „Typ B“ handelt. Soweit, so gut.
Nun aber kommt der dritte Entscheider an die Reihe. Er zieht eine rote Kugel, weiß aber, dass beide Entscheider vor ihm „Typ B“ gesagt haben, dass sie also vermutlich blaue Kugeln gezogen haben. Er wird daher vermuten, dass in 3 Experimenten zweimal blau und einmal rot vorkam, und seine Antwort lautet daher „Typ B“, obwohl er selbst eine rote Kugel gezogen hat. Nicht nur gibt er damit eine falsche Antwort, er kann damit auch die Information, über die er verfügte (nämlich dass er eine rote Kugel gezogen hat), nicht weitergeben.
Und jetzt läuft das Experiment aus dem Ruder, denn der vierte Entscheider sieht drei Vorgänger, die alle „Typ B“ gesagt haben. Im Grunde muss er nicht mal mehr ziehen – er wird sich als rationaler Entscheider in jedem Fall für „Typ B“ entscheiden. Und genauso alle Entscheider nach ihm – selbst wenn sie alle eine rote Kugel ziehen, wird keiner von ihnen seiner eigenen Information trauen, sondern die zahlreichen „Typ B“-Meldungen vor ihnen höher gewichten.
Ein einziges Ereignis zu Beginn des Experiments, das mit Wahrscheinlichkeit 1/9 eintritt, führt also dazu, dass sich alle Entscheider falsch entscheiden, weil jeder davon ausgeht, dass sich so viele vorherige Entscheider nicht irren können!
Bayes’sche Wahrscheinlichkeiten
Diese Überlegungen basieren auf dem sogenannten Bayes’schen Wahrscheinlichkeitsbegriff, der sich von dem unterscheidet, den man typischerweise in einer Stochastik-Vorlesung lernt. Dort geht man nämlich meist vom sogenannten frequentistischen Wahrscheinlichkeitsbegriff aus, nach dem eine Wahrscheinlichkeit eine relative Häufigkeit ist. Ein Experiment wie das obige unterstellt dagegen, dass die Entscheider die objektiven Wahrscheinlichkeiten ja gar nicht kennen können und dass sie daher stattdessen mit subjektiven Wahrscheinlichkeiten arbeiten, die ihrem Grad an persönlicher Überzeugung (englisch degree of belief) entsprechen.
An diesem Thema faszinieren mich zwei Punkte. Zunächst einmal bin ich tatsächlich fünfzig Jahre lang durch die Welt gegangen (davon mittlerweile über 20 als Wissenschaftler), ohne überhaupt etwas vom Glaubenskrieg zwischen Frequentisten und Bayesianern mitbekommen zu haben. Ich ertappe mich bei solchen Gelegenheiten gerne dabei, mich zu fragen, ob das jetzt an mir liegt oder ob es eine logische Folge des mittlerweile dermaßen unübersichtlich gewordenen Wissens auf der Welt ist und ob es anderen genauso geht.
Darüber hinaus handelt es sich hier aber möglicherweise tatsächlich um ein Werkzeug, um die beiden vermeintlich unvereinbaren Beobachtungen „Der Mensch verhält sich irrational“ und „Der Mensch hat es erfolgreich an die Spitze der Evolution geschafft“ miteinander zu vereinen. Womöglich ist der Mensch doch gar nicht so irrational, wie es manchmal scheint – er benutzt nur andere A-Priori-Wahrscheinlichkeiten als das Modell, gegen das seine Entscheidung getestet wird.
Zurück zur Informationskaskade
Auch wenn das obige Experiment natürlich ziemlich simpel ist, lassen sich ähnliche Überlegungen auf so manche Alltagssituation anwenden, wo wir unsere Hypothesen über die Wirklichkeit zum Teil aus eigener Beobachtung, zum Teil aber auch aus dem Verhalten anderer ableiten. Egal ob Reputationssysteme, Aktienmärkte oder schlicht unsere Einschätzung des neuen Kollegen – stets richten wir uns sowohl nach unserem eigenen Eindruck als auch nach den Aussagen Dritter. Das Ergebnis kann dann von Fehleinschätzungen (oder bewussten Manipulationen) gerade zu Beginn der Informationskette massiv verzerrt werden.
Diese Beobachtung steht im deutlichen Kontrast zur oft postulierten Wisdom of Crowds, derzufolge die Beteiligung vieler Informationsgeber zu besseren Entscheidungen führt. Während dies für Situationen stimmen mag, in der sich alle gleichzeitig ihre Meinung bilden (über die dann ein Mittelwert berechnet wird), ist es zweifelhaft, ob es auch korrekt ist, wenn sich Individuen bei der Meinungsbildung gegenseitig beeinflussen. Da die Art der Vernetzung der Entscheidungsträger dabei eine Rolle zu spielen scheint, wird das Thema nicht nur in der Verhaltensökonomik, sondern auch in der Netzwerkforschung (engl. Network Science) diskutiert. Und in dem Zusammenhang wird künftig sicherlich immer mal wieder in diesem Blog die Rede davon sein, denn dorthin scheint meine wissenschaftliche Reise gerade zu gehen – vielleicht schreibe ich in einem der nächsten Beiträge mehr dazu?