Haben Sie schon einmal vom Monty-Hall-Problem gehört? Falls nicht, eignet sich dieses mathematische Paradoxon als schönes Beispiel für eines meiner Lieblingsthemen in letzter Zeit, nämlich die Bedeutung des Praxistests für das Bilden von Theorien.
Das Monty-Hall-Problem
Das Monty-Hall-Problem wurde 1975 von dem amerikanischen Statistiker Steve Selvin vorgeschlagen und später von Craig F. Whitaker in seine heutige Form gebracht. Es kann wie folgt beschrieben werden:
Stellen Sie sich vor, Sie sind in der letzten Runde einer Game-Show. Sie stehen vor drei verschlossenen Türen und wissen, dass hinter einer davon ein Auto auf seinen Gewinner wartet, hinter den beiden anderen aber lediglich eine Ziege. Obwohl Sie zunächst keine weiteren Informationen haben, müssen Sie sich für eine Tür entscheiden.

Nachdem Sie vor der gewählten Tür stehen, öffnet der Showmaster eine der anderen Türen, hinter der (natürlich) eine Ziege steht. Dann stellt er Ihnen die Frage, ob Sie Ihre Wahl jetzt noch ändern und lieber die andere Tür wählen wollen. Wie würden Sie sich entscheiden?
Zwei Sichtweisen
Zwei Argumentationen auf dieses Problem sind besonders verbreitet.
- Strategie A: Viele Menschen argumentieren, dass jetzt ja nur noch zwei Türen übrig sind und dass die Wahrscheinlichkeit für ein Auto jeweils 1/2 für jede der Türen beträgt. Es macht also keinen Sinn, die ursprüngliche Entscheidung zu revidieren.
- Strategie B: Manche argumentieren dagegen, dass die Wahrscheinlichkeit, im ersten Schritt die richtige Tür gewählt zu haben, 1/3 betrug. Die Wahrscheinlichkeit, dass das Auto hinter einer der anderen Türen steht, beträgt somit 2/3. Und daran ändert sich auch nichts, wenn der Showmaster eine Ziegentür öffnet. Es macht also Sinn, die Tür zu wechseln, weil die Wahrscheinlichkeit, dass das Auto hinter der der anderen Tür steht, nun 2/3 beträgt.
Natürlich kann man diese Überlegungen auch deutlich mathematischer aufschreiben, und genau das wurde auch getan. So hat die Kolumnistin Marilyn vos Savant in ihrer Kolumne „Ask Marilyn“ für Strategie B argumentiert und dafür ca. 10.000 Leserbriefe (darunter über 1000 Verfasser mit einem Doktortitel in Mathematik) erhalten, in denen erklärt wurde, warum sie falsch liegt und Strategie A richtig ist.
Der Praxistest
Tatsächlich ist Strategie 2 richtig, und natürlich kann man das auch mathematisch beweisen. Aber die bloße Tatsache, wie viele intelligente Menschen sich hier zunächst täuschen ließen und dafür auch gute Argumente fanden, zeigt, wie gefährlich eine reine Beschränkung auf die Theorie ist.
Als Informatiker kommt mir da natürlich recht schnell der Gedanke, das eigene mathematische Modell durch eine Rechnersimulation zu verifizieren. So führt der folgende Python-Code 1000 Versuche durch, bei denen Spieler A seine Tür beibehält und Spieler B die Tür wechselt:
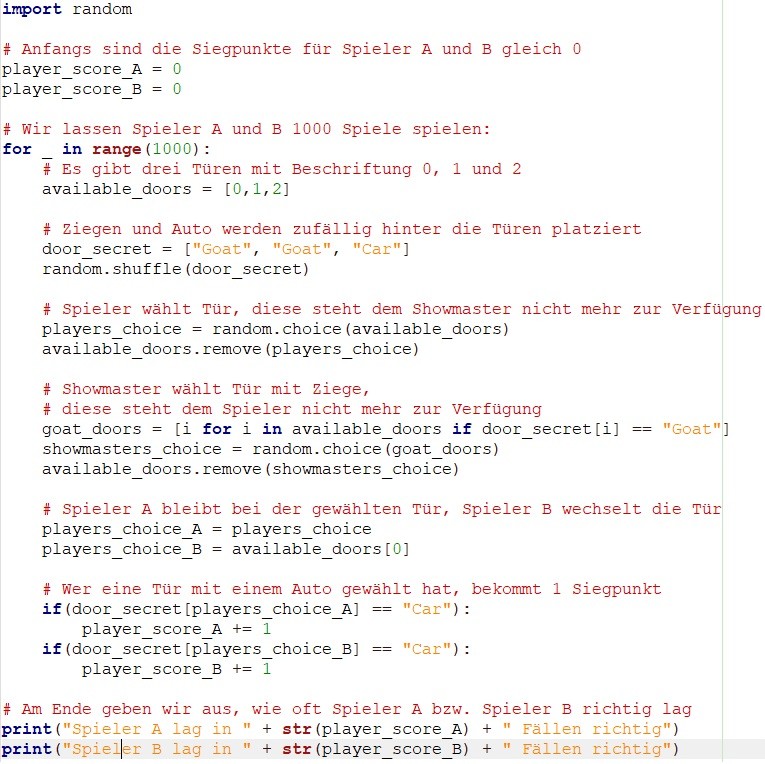
Ein Beispiellauf dieses Programms erzeugt das folgende Output:

Wie man sieht, hätte man die Lösung also auch ohne den Hauch eines mathematischen Verständnisses einfach durch Ausprobieren finden können: Strategie B hat eine deutlich höhere Erfolgswahrscheinlichkeit!
Die Sache mit den Tauben
Es kommt aber noch schlimmer. Walter Herbranson und Julia Schroeder veröffentlichten im Jahr 2010 ein Paper zu einem Monty-Hall-Experiment, das sie mit Tauben durchgeführt hatten. Der Artikel trägt den schönen Titel „Are Birds Smarter Than Mathematicians? Pigeons (Columba livia) Perform Optimally on a Version of the Monty Hall Dilemma“ und beschreibt eine Reihe von Versuchen zu ebendiesem Thema.
Bereits das erste davon ist gewissermaßen die taubengerechte Variante des Monty-Hall-Problems (mit Futter statt Autos, Futterklappen statt Türen und Lichtern statt Showmastern). Anfangs hatten die Tiere 10 Versuche pro Tag, die dann auf bis zu 100 Versuche gesteigert wurden. Dabei stellte sich heraus, dass die Tiere zu Beginn nur mit 36% ihre Wahl änderten, am 30. Tag der Versuchsreihe aber in 96% der Fälle. Sie hatten also durch Versuch und Irrtum gelernt, dass das Ändern der ursprünglichen Wahl die optimale Strategie für das Monty-Hall-Problem darstellt.
Ausprobieren nicht vergessen!
Natürlich kann man jetzt polemisch werden und sagen: Tauben sind klüger als Mathematiker oder auch als Menschen allgemein (denn es gibt auch Studien, die belegen, dass Menschen erstaunlich hartnäckig bei ihrer ursprünglichen Wahl bleiben). Was natürlich so nicht stimmt, aber das Ergebnis sollte uns zumindest zu denken geben.
Die wichtige Erkenntnis, die für mich in den Betrachtungen zum Monty-Hall-Problem steckt, ist: Ganz gleich, wie elegant eine Theorie ist – man sollte sie ab und zu einem Praxistest unterziehen. Und zwar ganz egal, ob man ein Wissenschaftler ist, der über entscheidungstheoretische Dilemmata nachsinnt, oder ein ganz normaler Mensch, der ein mentales Modell seiner Umwelt entwickelt.
Das mag völlig selbstverständlich klingen, ist es aber nicht. Im Gegenteil: In Zeiten von Filterblasen, politischer und religiöser Radikalisierung, Konstruktivismus, Haltungsjournalismus und sogar Wissenschaften, die andere Meinungen lieber niederschreien als sich ernsthaft mit ihnen auseinanderzusetzen, scheint mir dieser Appell aktueller zu sein denn je.
Wir sind in der Lage, in unserem eigenen Kopf beliebig plausibel klingende Modelle unserer Umwelt zu entwickeln. Ob es sich aber auch um gute Modelle handelt, entscheidet nicht die Eleganz der Argumentation, sondern ihre Vorhersagekraft in der wirklichen Welt. Oder wie man im Angelsächsischen sagt: „The proof of the pudding is in the eating“.